初中数学三大函数：一次函数，反比例函数，二次函数。二次函数河南中考压轴题地位不可动摇，通常三问，单独的抛物线总是“寂寞”的，基本都会有一次函数的陪伴，二次函数与反比例函数基本不会涉及。但是有关反比例函数的问题时常在中考中也会出现，并呈现出愈加灵活的趋势，成为中考考查的重点之一，在解反比例函数问题时，灵活运用比例系数k的几何意义，通过题目中的函数条件或几何图形，理解函数的图象或借助于图形的直观性从中找出正确答案，在中考的战场中拿下这个考点。让我们一起来全面了解反比例的考情和K的几何意义的“千娇百态”的变形。

1--考情

2--知识点：反比例函数中k 和几何意义：

反比例函数y=k/x(k非0)中，比例系数k的几何意义，就是过该函数图像上任一点P（x，y）分别作x轴、y轴的垂线PM，PN，垂足为M、N，所得矩形PMON的面积S 矩形PMON = PM・PN = |x|・|y| = |xy| = |K|，即过曲线上任意一点作x轴、y轴的垂线，所得到的矩形的面积为常数|K|，这是系数K几何意义。

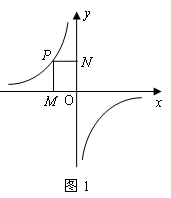
同时通过K性质可以延伸出多种图形面积的不变性特征，如下：

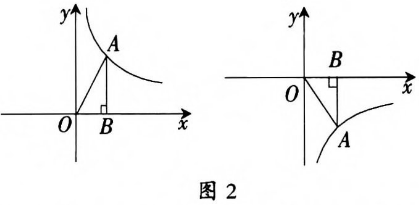
①三角形面积的不变性 如图右图所示，S△AOB=1/2|k|
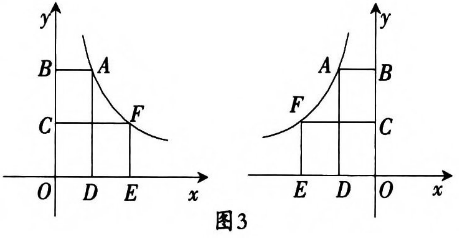
②矩形面积的不变性 如图右图所示，S 矩形ABOD =S 矩形COEF =|k|
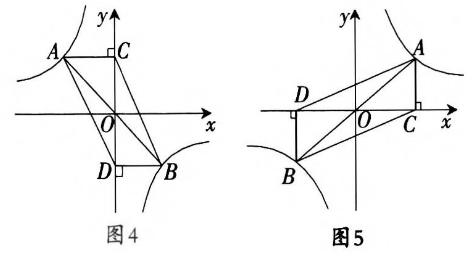
③平行四边形面积的不变性 如图右图所示，AC∥x轴，或AC∥y轴 S 平行四边行ADBC =2|k|（点A与点B关于原点O对称）

有益补充：

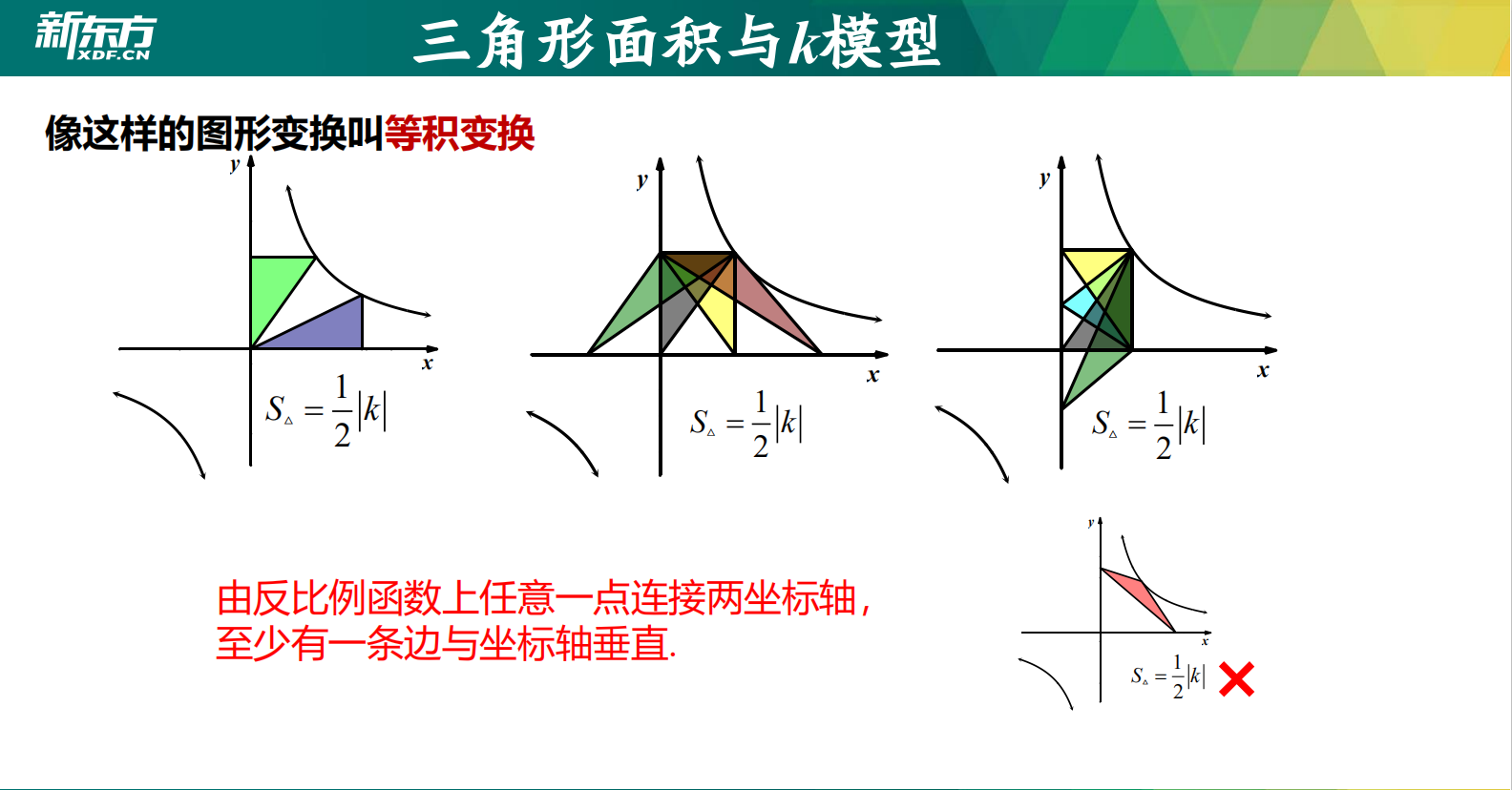
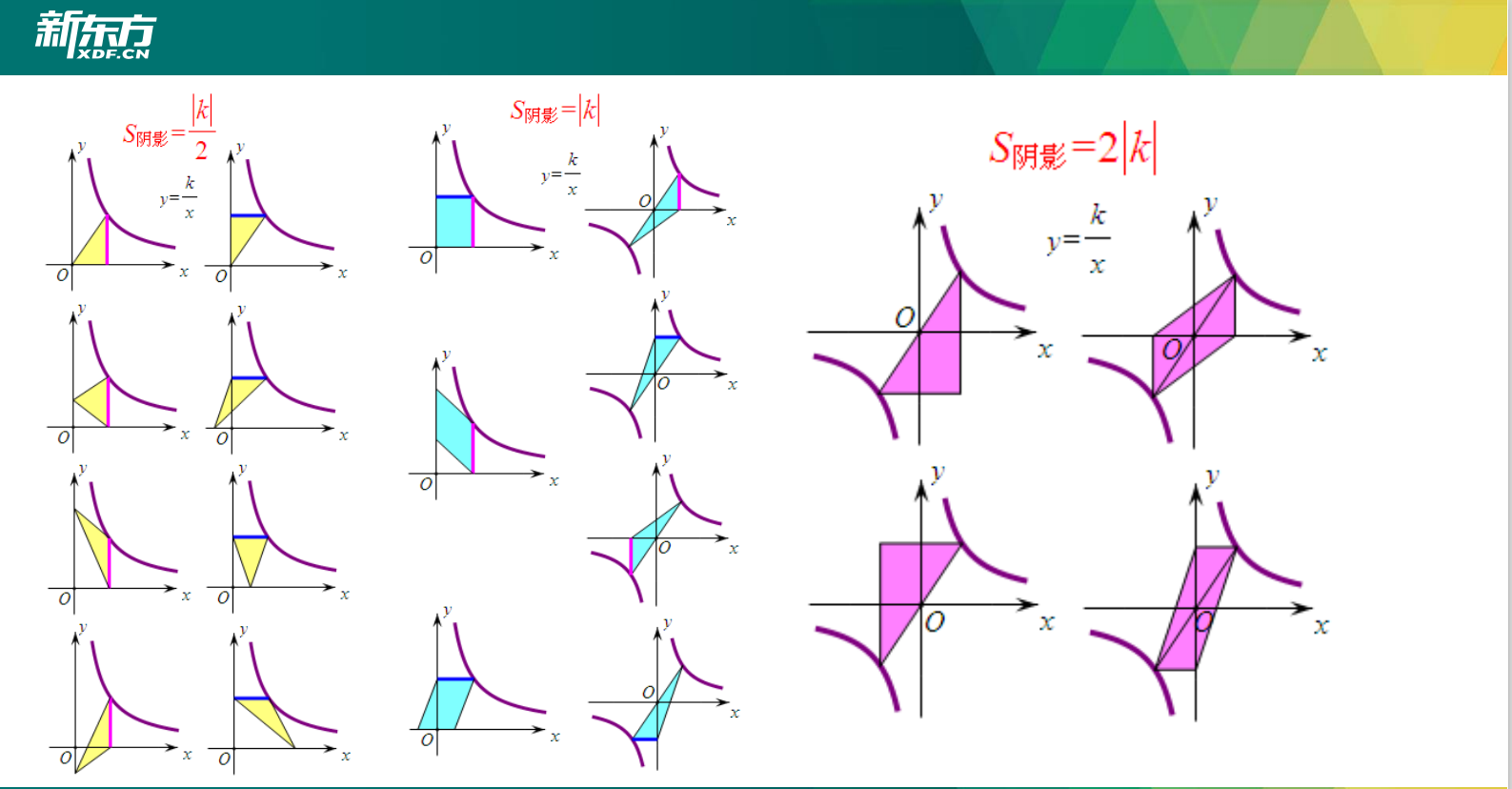
明确了K的几何意义，会提高孩子们对于此类类型的题目的做题速度和准确度。

三：实战应用一二

例题1：如图，A、B两点在双曲线y＝4/x上，分别经过A、B两点向坐标轴作垂线段，已知S阴影＝1.7，则S1+S2等于（　　）

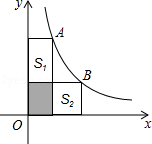
A．4         B．4.2         C．4.6         D．5

考点：反比例函数系数K的几何意义。

分析：根据反比例函数系数K的几何意义可得S四边形AEOF＝4，S四边形BDOC＝4，根据S1+S2＝S四边形AEOF+S四边形BDOC﹣2×S阴影，可求S1+S2的值．

解答：如图，∵A、B两点在双曲线y＝4/x上，

∴S四边形AEOF＝4，S四边形BDOC＝4，

∴S1+S2＝S四边形AEOF+S四边形BDOC﹣2×S阴影，

∴S1+S2＝8﹣3.4＝4.6

故选：C．

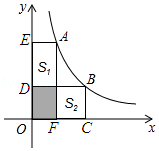
点评：本题考查的是反比例函数系数k的几何意义。

例题2：反比例函数y=6/x与y=3/x在第一象限的图象如图所示，作一条平行于x轴的直线分别交双曲线于A、B两点，连接OA、OB，则△AOB的面积为（　　）

A.3/2         B.2         C.3          D.1

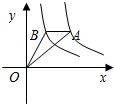
考点：反比例函数系数k的几何意义。

分析：分别过A、B作x轴的垂线，垂足分别为D、E，过B作BC⊥y轴，点C为垂足，再根据反比例函数系数k的几何意义分别求出四边形OEAC、△AOE、△BOC的面积，进而可得出结论．

解答：分别过A、B作x轴的垂线，垂足分别为D、E，过B作BC⊥y轴，点C为垂足，

∵由反比例函数系数k的几何意义可知，S四边形OEAC=6，S△AOE=3，S△BOC=3/2，

∴S△AOB=S四边形OEAC﹣S△AOE﹣S△BOC=6﹣3﹣3/2=3/2．故选A．

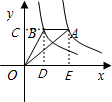
点评：本题考查的是反比例函数系数k的几何意义。